Record player - Null Points
Making the Adjustment

D Vautier
07/2017
email

General

When a record is made the cutter cuts across the master tangent to the groove (90 degrees).  So when playing we try to get the cartridge to play as close to that same tangent angle as we can.  This is done by the manipulation of overhang and attack angle.  With proper adjustment it is quite possible to get pretty close to tangent, maybe within zero to five degrees over the entire playing surface of a record. 

Null point alignment is the first and most basic adjustment to be made when installing a cartridge on a turntable.  It sometimes can make noticeable differences in sound quality especially at the higher end and determines overhang which also controls the anti-skating force.  It is perhaps the most overlooked adjustment because often cartridges are not sold with adequate alignment tools and the alignment process can be tedious to understand and perform.

It should also be understood that manufacturers design their product with one preferred alignment in mind, even though the user is free to choose other alignments because just about all TTs allow both overhang an attack angle adjustment.  But the tools provided are usually designed for just one type alignment and usually only consider overhang.

Furthermore alignment tools often overlook the cartridge cantilever which is not the same as the cartridge body.  Cantilevers are the best measure of tangency and are constantly subjected to pressure during their useful life not just from the groove but from skating and anti-skating forces that vary over the record surface.  It is therefore not uncommon to note that a cantilever may not be quite parallel to the cartridge shell.  This is perfectly expected and doesn't necessarily degrade performance.

It is also quite common to see alignment tools that only adjust overhang and ignore cartridge angle.  This is unfortunate but then a lot of average users do not want to get involved in the esoteric art of complex geometrics.   

Most turntables are designed with a bend in the tonearm of between 26 and 30 degrees which can be built into the arm itself or into the headshell. Some arms have no headshells. The arm overhangs the spindle by around 12 to 14 percent of the pivot length (pivot to spindle, or PtoS). Longer arms require less overhang and result in bigger null points. The PtoS is a constant which is built into the turntable by the manufacturer and is defined as the distance from arm pivot to spindle center.  Arm length (effective length) here means the actual distance from pivot to stylus and this is usually adjustable and can change the overhang.

Turntables are designed with angular arms and overhang as a way to increase the apparent arm length and thus reduce tangential error since the apparent arm length is projected out to be longer than the actual arm length.  In the diagram here we observe an apparent arm length which is approximately 1 and 1/2 longer than the actual arm length. It’s just geometry, not style, convenience, tradition or magic, but it's been done this way since stereo came along and tangency became more important in separating the two channels. 

There are two points on a properly adjusted turntable where the tangent becomes zero, that is, when the stylus rides in the groove at exactly the right angle.  These are called null points.  Null points are determined by cartridge angle and arm length (actual arm length).  Arm length can be adjusted quite a bit on tonearms with standard headshells but arms without headshells have little ability to change arm length unless they have slotted mounting holes.  Many of them do.  Changing arm length also changes overhang. This significantly effects null point adjustment.  The ratio between PtoS and overhang is just as important as cartridge angle.

Here is a standard headshell.  the cartridge mounting slots are about 12 mm long.

Changing arm length changes distance between null points.  Changing the attack angle of the cartridge moves the null points together in or out from center but both these adjustments work somewhat together, and to get null points where you want them requires manipulating both arm length and attack angle a number of times.  The objective is that a record is best played with a minimum amount of tangential error across the entire playing surface, or better said, the stylus should remain as perpendicular as long as possible during play.

Here is a picture of the issue (not to scale)

Description

As mentioned above, null points can be moved by a combination of lengthening or shortening arm length and adjusting the attack angle of the cartridge which is mounted in a headshell and is already at some angle.  Since a standard headshell allows about 11 to 13 mm arm length change and up to 15 degrees angle change, it is quite possible to arrive at just about any set of null points you may want.

However, the effective playing area begins at 145 mm from center and ends at 65 to 70 mm from center.  There are few record manufacturers today that dare cut closer than 65 mm from center.  Even though the inner groove standard is supposed to be 60.325 mm from center, many turntables will go into return cycle before that point.  It is for this good reason that no record is cut closer than 65 mm from center, even though high end turntables usually have no return mechanism so they don't have to worry about the amount of deadwax.

Published Null Points

The three advertized alignments and their null points are:

Baerwald 66 and 120.9
Loefgren 70.3 and 116.6
Stevenson 60.325 and 117.42

From what it seems Baerwald tries to even out all distortion by attempting to spread it out in the middle.  Loefgren minimizes distortion by trying to average it out over the entire record and Stevenson reduces distortion by favoring the inner groves which may be more compact and more in need of alignment.  Manufacturers may recommend one of the other type but I have a hard time seeing why it would matter.

Basically none of these alignments make a lot of sense to me because they calculate a final groove at 60.325 which is not borne out by fact.  Records are just not cut that way anymore.  Deadwax begins way before 60 mm, usually around 68 or 69 mm which is even pushing it.  My calculations come up with a preference for an 85 and 120 mm null setting given that I do favor the inner grooves a bit.  But this takes into account an actual playing area of 147 to 70 mm rather than the hypothetical 145 to 60 that the methods above are probably using.

Make The Template

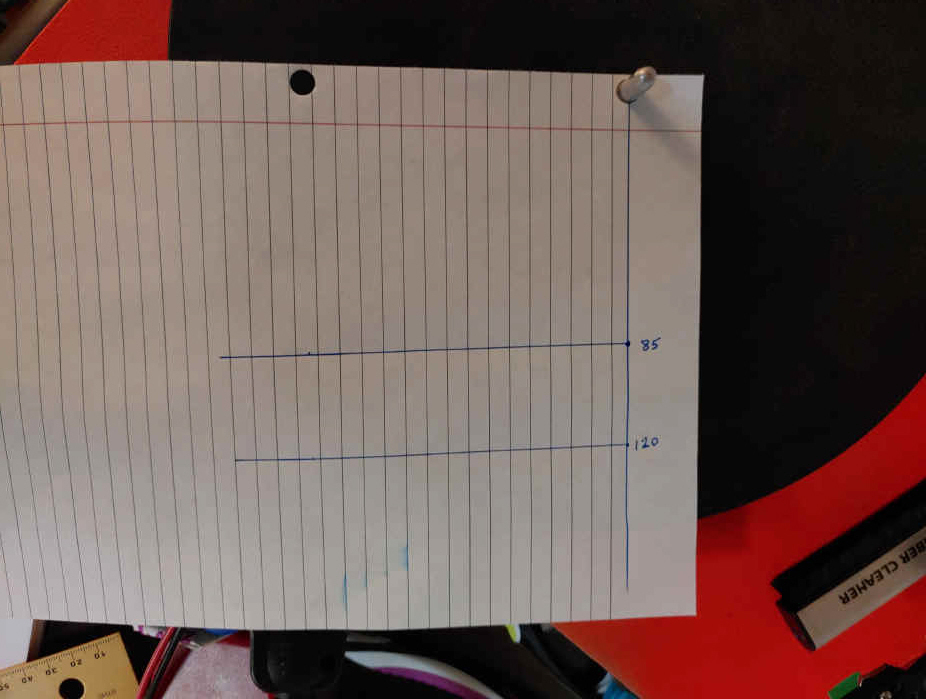
Take a sheet of lined paper and punch a hole on the upper right side on the top line or use one of the holes.  This becomes the spindle center and the line becomes your index line.  Then mark your preferred null points on the index line.  Here I use my null points (85-120) but you may want to use your own nulls like 90-125, which would emphasize the second and forth piece on a five selection side, or perhaps an 80-115 which gets a fatter part of the surface.  Project a right angle out from your two points. You now have your template. 

Make The Pointer

Now you need a way to project the true perpendicular from the cartridge cantilever onto the template.  The pointer is mounted on the body of the cartridge and moves as the cartridge is adjusted.  If your cartridge does not come with a pointer you can make one with a paper clip just so the tip of the pointer lines up with the cantilever.  I used a paperclip in this example.  The picture is at an angle so it looks a little off.  Just the tip has to line up.  Not the whole thing.  In this example I used my custom homemade TT and the optimum attack angle was about 10 degrees which is pretty excessive.  In a production TT the attack angle is often close to zero.

Do The Test

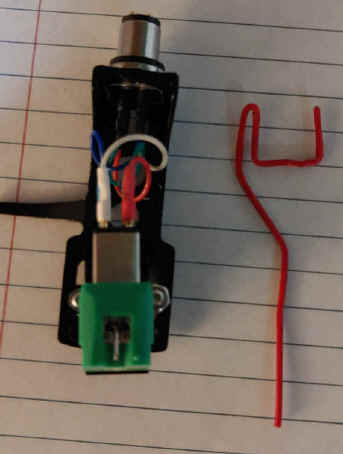
There are various techniques described everywhere for null point adjustment and I think it may depend on the turntable, tonearm and cartridge but it does involve a template, a number of repetitive length and angle adjustments and then some performance listening.  As described above, changing the arm length will increase or decrease the tracking arc thus moving the null points closer or farther apart.  Rotating the cartridge will move the null points in and out and somewhat effect the distance between points. When the distance between your null points is good your overhang is good.  Rotating the angle of the cartridge changes the position of the two points.
Here's an interesting experiment. I first extended the cartridge out to the very end of the headshell giving the arm a maximum length just to see what would happen. It was really bad. I then adjusted to the middle of my headshell and began to change the angle until I got my inner null point and then repeated the process against the outer null point.  When I got satisfactory adjustments of both points I aligned the pointer to the position of the cartridge and marked off each angle.  If your pointer is taped to the headshell you have to readjust it every time you change the angle of the cartridge by sighting down the cartridge to the cantelever, fixing the pointer over the stylus and adjusting the far end of the pointer until it aligns with the new stylus angle. That can be a pain.

When taking measurements it is important to carefully sight down the spindle axis to make sure that your stylus is right on the index line because this makes a huge difference in the tangent angle.  Then place the stylus exactly on its point lock the TT with some cardboard and mark off the displacement.

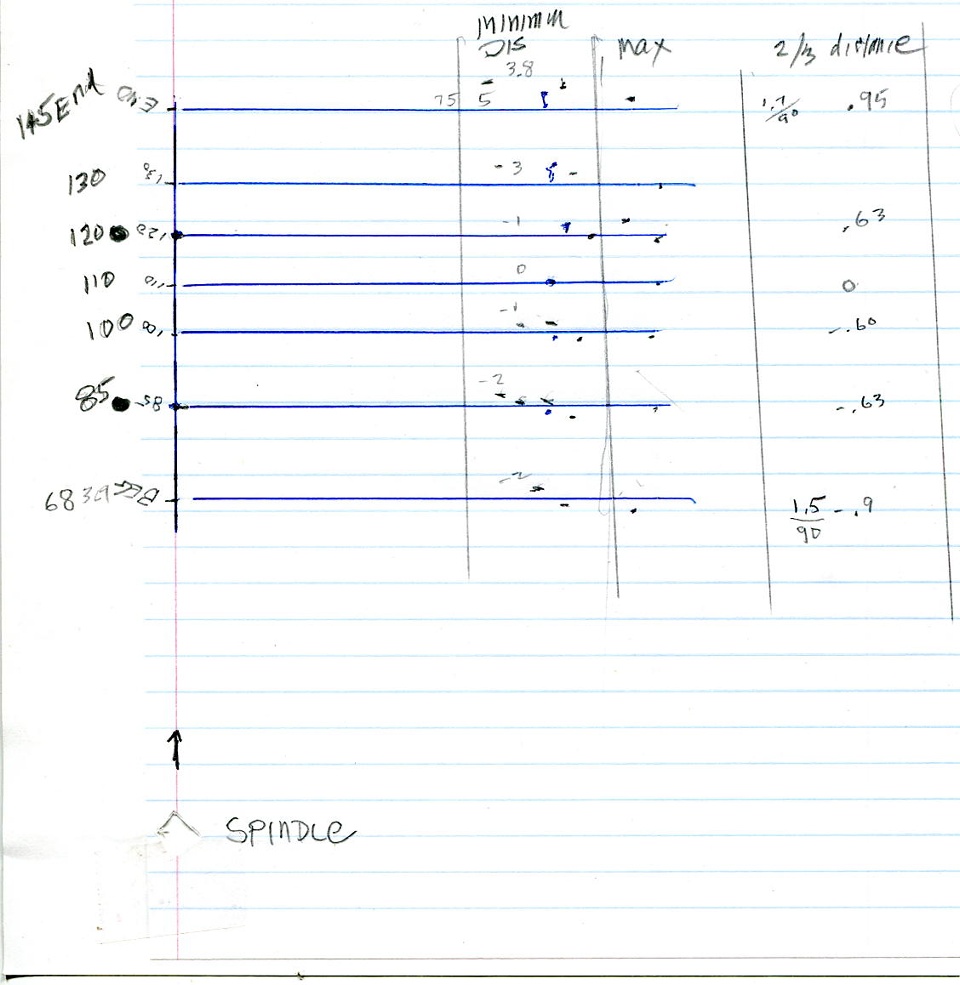
Next I moved the cartridge all the way up on the headshell to get the shortest arm length and repeated the tests. It was hard to get null points at both extremes but it gave me a general idea where the "soft spot" was.  I decided that about 2/3rds down the headshell was about the best spot and it generally is.  I did a third set of tests at that location.  The results were quite satisfactory because all readings were within one degree of tangent (and that is damn good).

Another perhaps simpler technique can be described like this.  Position the cartridge midway on the headshell at zero degrees rotation (straight up).  Place the pointer and tool.  Now by moving the arm and tool discover and mark the location of current null points.  From here you can make what additional adjustments are needed.  Remember that an arm length change moves the nulls closer or farther apart.  Angle change moves both nulls in or out.
 

Here is my final cartridge adjustment.  It is about 5 degrees clockwise and about 1/3 of the way down the adjusting slot.
 

Here I'm checking the alignment of the pointer with a ruler just to make sure that it is on line with the side of the cartridge.
 

Here is my template/worksheet. I started by finding the null points with cartridge midway and at zero rotation.  The distance between the nulls was too much so I gradually brought the cartridge back till I got 35mm.  I then rotated the cart to bring the nulls to 85 and 120.

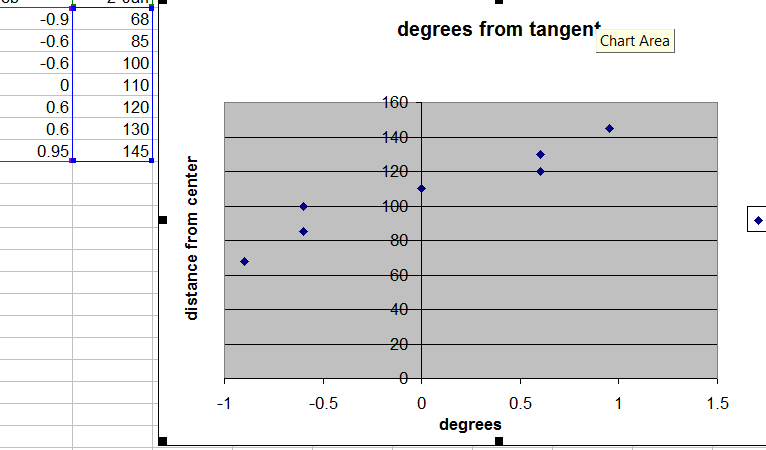
Here is a scatter chart of tangent error taken at minimum arm length.

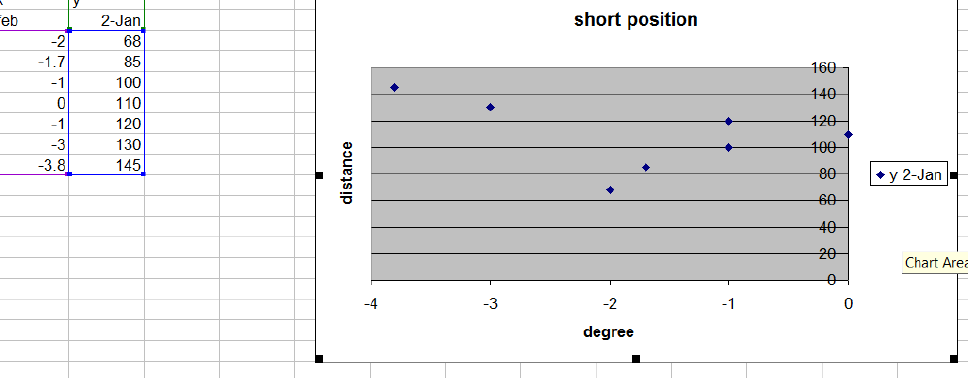
Here is a scatter chart of the optimum tangent error.  All samples are within one degree.